Master of Science in Mathematics, 2018
1: Preface
Pursuant to Act 172 of February 27, 2018 on Universities (the University Act) with subsequent changes, the following curriculum is stipulated. The programme also follows the Joint programme regulations and the Examination Policies and Procedures for The Faculty of Engineering and Science, The Faculty of Medicine and The Technical Faculty of IT and Design.
2: Basis in Ministerial orders
The Master’s programme is organised in accordance with the Ministry of Higher Education and Science’s Order no. 1328 of November 15, 2016 on Bachelor’s and Master’s Programmes at Universities (the Ministerial Order of the Study Programmes) and Ministerial Order no. 1062 of June 30, 2016 on University Examinations (the Examination Order). Further reference is made to Ministerial Order no. 111 of January 30, 2017 (the Admission Order) and Ministerial Order no. 114 of February 3, 2015 (the Grading Scale Order) with subsequent changes.
3: Campus
The programme is offered in Aalborg.
4: Faculty affiliation
The Master’s programme falls under The Faculty of Engineering and Science, Aalborg University.
5: Study board affiliation
The Master’s programme falls under Study Board of Mathematical Sciences
6: Affiliation to corps of external examiners
The Master’s programme is associated with the Body of External Examiners for Mathematics (Censorkorpset for matematik).
7: Admission requirements
Applicants with a legal claim to admission (retskrav):
Applicants with one of the following degrees are entitled to admission:
- Bachelor of Science (BSc) in Mathematics, Aalborg University
Applicants without legal claim to admission:
- Bachelor of Science (BSc) in Mathematics, Aarhus University (AU)
- Bachelor of Science (BSc) in Mathematics, Copenhagen University (KU)
- Bachelor of Science (BSc) in Mathematics, Southern Danish University (SDU)
8: The programme title in Danish and English
The Master’s programme entitles the graduate to the Danish designation Cand.scient. i matematik. The English designation is: Master of Science (MSc) in Mathematics.
Or
Cand.scient. (candidatus/candidata scientiarum) i matematik og [sidefag]. The English designation is: Master of Science (MSc) in Mathematics and [Minor Subject].
9: Programme specifications in ECTS credits
The Master’s programme is a 2-year, research-based, full-time study programme. The programme is set to 120 ECTS credits.
10: Rules concerning credit transfer (merit), including the possibility for choice of modules that are part of another programme at a university in Denmark or abroad
The Study Board can approve successfully completed (passed) programme elements from other Master’s programmes in lieu of programme elements in this programme (credit transfer). The Study Board can also approve successfully completed (passed) programme elements from another Danish programme or a programme outside of Denmark at the same level in lieu of programme elements within this curriculum. Decisions on credit transfer are made by the Study Board based on an academic assessment. See the Joint Programme Regulations for the rules on credit transfer.
11: Exemptions
In exceptional circumstances, the Study Board study can grant exemption from those parts of the curriculum that are not stipulated by law or ministerial order. Exemption regarding an examination applies to the immediate examination.
12: Rules for examinations
The rules for examinations are stated in the Examination Policies and Procedures published by the faculty on their website.
13: Rules concerning written work, including the Master’s Thesis
In the assessment of all written work, regardless of the language it is written in, weight is also given to the student's formulation and spelling ability, in addition to the academic content. Orthographic and grammatical correctness as well as stylistic proficiency are taken as a basis for the evaluation of language performance. Language performance must always be included as an independent dimension of the total evaluation. However, no examination can be assessed as ‘Pass’ on the basis of good language performance alone; similarly, an examination normally cannot be assessed as ‘Fail’ on the basis of poor language performance alone.
The Study Board can grant exemption from this in special cases (e.g., dyslexia or a native language other than Danish).
The Master’s Thesis must include an English summary (or another foreign language: French, Spanish or German upon approval by the Study Board). If the project is written in English, the summary must be in Danish (The Study Board can grant exemption from this). The summary must be at least 1 page and not more than 2 pages (this is not included in any fixed minimum and maximum number of pages per student). The summary is included in the evaluation of the project as a whole.
14: Requirements regarding the reading of texts in a foreign language
It is assumed that the student can read academic texts in his or her native language as well as in English and use reference works etc. in other European languages.
15: Competence profile on the diploma
The following competence profile will appear on the diploma:
A Candidatus graduate has the following competency profile:
A Candidatus graduate has competencies that have been acquired via a course of study that has taken place in a research environment.
A Candidatus graduate is qualified for employment on the labour market based on his or her academic discipline as well as for further research (PhD programmes). A Candidatus graduate has, compared to a Bachelor, developed his or her academic knowledge and independence so as to be able to apply scientific theory and method on an independent basis within both an academic and a professional context.
16: Competence profile of the programme
Students graduating as Masters of Mathematics
Knowledge
- are well-oriented in the foundations of key mathematical disciplines including mathematical analysis, algebra, geometry, probability and statistics
Skills
- are able to independently identify, formulate and analyse mathematical problems employing theory and methodology from the mathematical sciences
- are able to independently choose relevant methods and tools from various mathematical areas and to motivate this choice
- are able to disseminate scientific knowledge and to discuss applications of methods from the mathematical sciences
Competencies
- are able to ponder about central mathematical insights, methods and tools and to identify problems amenable to mathematical treatment
- are able to manage complex work and development scenarios that may require new strategies in order to make progress
- are able to independently take responsibility for professional development and specialization
Moreover, graduates within Applied Mathematics
Knowledge
- have acquired a profound understanding within one or a few mathematical areas linking up to international research level
Skills
- can apply techniques of mathematical modelling to theories and problems originating in scientific areas from outside of Mathematics
- are able to choose relevant mathematical theories to problems that originate in, for example, engineering, computer science or economics, to develop them and to make use of them in the original applied context
Competencies
- are able to launch and to perform professional and responsible scientific collaboration with peers from within and from outside of Mathematics
Moreover, students graduating in Mathematics in combination within a second subject
Knowledge
- have acquired a broad view into mathematical theories and methods within several mathematical areas and their mutual connections
Skills
- are able to disseminate scientific knowledge to non-experts and to reflect about best practices how to achieve good understanding
Competencies
- are able to identify requirements for their further development of scientific knowledge and methodology and to structure ways of achieving requested insights
17: Structure and Contents of the programme
The programme is structured in modules and organized as a problem-based study. A module is a programme element or a group of programme elements, which aims to give students a set of professional skills within a fixed time frame specified in ECTS credits, and concluding with one or more examinations within specific exam periods. Examinations are defined in the curriculum. The programme is based on a combination of academic, problem-oriented and interdisciplinary approaches and organized based on the following work and evaluation methods that combine skills and reflection:
- lectures
- classroom instruction
- project work
- workshops
- exercises (individually and in groups)
- teacher feedback
- reflection
- portfolio work
General provisions concerning elective courses:
- Only a limited number of elective courses from the list of courses will be offered at each semester.
- Students can only participate once in a course with a given title. In particular, they cannot follow a course if they have previously participated in a course with the same title as part of a bachelor programme.
PBL Introductory Course
All students who have not participated in Aalborg University’s PBL introductory course during their Bachelor’s degree must attend the introductory course “Problem-based Learning and Project Management”. The introductory course must be approved before the student can participate in the project exam. For further information, please see the School of Engineering and Science’s website.
The two-disciplinary Master’s degree in Mathematics is planned in accordance with the guideline for academic minimum required standards for university programmes directed towards teaching.
The two-disciplinary master’s degree fulfills the below described academic minimum required standards:
”Det er en forudsætning for, at en kandidat kan opnå faglig kompetence i faget matematik i de gymnasiale uddannelser, at kandidaten opfylder de nedenfor beskrevne faglige mindstekrav.
Kandidatens uddannelse skal omfatte studieaktiviteter med et samlet omfang på 120 ECTS-point, indeholdende:
– obligatorisk kernestof på mindst 60 ECTS-point,
– dybdestof på op til 30 ECTS-point,
– breddestof på ca. 20 ECTS-point og
– fagdidaktik og videnskabsteori på ca. 10 ECTS-point.
Mål
Kandidaten skal have indgående kendskab til udvalgte faglige områder af betydning for fagets udvikling og forskning i faget. Kandidaten skal selvstændigt kunne anvende faget i komplekse sammenhænge, herunder:
- analysere en matematisk problemstilling med anvendelse af tankegange, ræsonnementer og repræsentationsmåder, der er karakteristiske for matematik.
- perspektivere faglige indsigter og belyse matematikkens samspil med den historiske, kulturelle og teknologiske udvikling.
- kende, kunne udvikle og behandle matematiske modeller og kritisk kunne diskutere deres gyldighed.
- med udgangspunkt i sit faglige overskud kunne formidle matematikfaglige emner til en udvalgt målgruppe med inddragelse af visuelle eller beregningstekniske hjælpemidler.
Fagligt stof
Obligatorisk kernestof
Kandidaten skal have formel forståelse af følgende faglige emner med nogenlunde samme vægt:
- differential- og integralregning, herunder differentialligninger.
- matematisk analyse.
- geometri.
- lineær algebra.
- algebra.
- sandsynlighedsteori og statistik.
- diskret matematik.
Dybdestof
Stoffet skal perspektivere og videreføre progressionen af de faglige emner fra kernestoffet. Emnerne vælges inden for en af universitetet fastsat liste, og den bør omfatte et eller flere videregående faglige emner, der inddrager matematisk modellering og uddyber eller supplerer kernestoffet.
Breddestof
I breddeaktiviteterne skal indgå:
- matematikkens historie.
- programmering, der supplerer et eller flere kernestofemner.
- matematisk behandling af problemstillinger hentet fra andre fagområder, herunder naturvidenskab”
18: Overview of the programme
All modules are assessed through individual grading according to the 7-point scale or Pass/Fail. All modules are assessed by external examination (external grading) or internal examination (internal grading or by assessment by the supervisor only).
Students can participate only once in a course with a given title. In particular, they cannot follow a course if they have previously participated in a course with the same title as part of a bachelor programme.
Offered as:
1-professional | |||||
| Study programme: Applied Mathematics | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation method | Assessment method |
1 Semester
| |||||
| Introductory Application Oriented Mathematics | Project | 15 | 7-point grading scale | External examination | Oral exam based on a project |
| MAT7 elective courses | Course | 15 | |||
2 Semester
| |||||
| Intermediate Application Oriented Mathematics | Project | 15 | 7-point grading scale | Internal examination | Oral exam based on a project |
| MAT8 elective courses | Course | 15 | |||
3 Semester
| |||||
| Advanced Application Oriented Mathematics | Project | 20 | 7-point grading scale | Internal examination | Oral exam based on a project |
| MAT9 elective courses | Course | 10 | |||
3-4 Semester
| |||||
| Long Master’s Thesis. 50 ECTS | Project | 50 | 7-point grading scale | External examination | Oral exam based on a project |
| Long Master’s Thesis, 60 ECTS | Project | 60 | 7-point grading scale | External examination | Oral exam based on a project |
4 Semester
| |||||
| Master’s Thesis. 30 ECTS | Project | 30 | 7-point grading scale | External examination | Oral exam based on a project |
Elective courses
In stead of the courses listed here (Elective courses on MAT7, MAT8 and MAT9) the student may follow courses from different curricula, e.g. engineering or computer science, as discribed in the Competence profile for Applied Mathematics.
The student selects courses equivalent to 15 ECTS on the 1'st semester (MAT7). Only a limited number of elective courses will be offerede each semester.
MAT7 elective courses | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation Method | Assessment method |
| Introduction to Partial Differential Equations | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Numerical Analysis | Course | 5 | Passed/Not Passed | Internal examination | Oral exam |
| Manifolds – Differential Geometry and Topology | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Optimization | Course | 5 | 7-point grading scale | External examination | Written or oral exam |
| Measure Theory and Stochastic Processes | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Statistics for Duration Data | Course | 5 | Passed/Not Passed | Internal examination | Active participation/continuous evaluation |
| Topics in Statistical Sciences I | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Topics in Statistical Science II | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Information and Coding Theory | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
The student selects courses equivalent to 15 ECTS on the 2'nd semester (MAT8). Only a limited number of elective courses will be offerede each semester.
MAT8 elective courses | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation Method | Assessment method |
| Bayesian Inference and Mixed Models | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Time Series and Econometrics | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Spatial Statistics and Markov Chain Monte Carlo Methods | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Graph Theory | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Coding Theory | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Applied Harmonic Analysis | Course | 5 | Passed/Not Passed | Internal examination | Oral exam |
| Operators on Hilbert Spaces | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Algebraic Topology | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Quantitative Finance and Computational Statistics | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Financial Engineering | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Data Mining | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Compressive Sensing | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
The student selects courses equivalent to 10 ECTS on the 3'rd semester (MAT9). Only a limited number of elective courses will be offerede each semester.
MAT9 elective courses | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation Method | Assessment method |
| Introduction to Partial Differential Equations | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Numerical Analysis | Course | 5 | Passed/Not Passed | Internal examination | Oral exam |
| Manifolds – Differential Geometry and Topology | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Optimization | Course | 5 | 7-point grading scale | External examination | Written or oral exam |
| Measure Theory and Stochastic Processes | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Statistics for Duration Data | Course | 5 | Passed/Not Passed | Internal examination | Active participation/continuous evaluation |
| Topics in Statistical Sciences I | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Topics in Statistical Science II | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Information and Coding Theory | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Topics in Algebraic Geometry and Commutative Algebra | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Topics in Applied Mathematical Analysis and Geometry | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
Study abroad
On the 3'rd semester the student also has the possibility to study at another Danish or international university (study abroad). Study at another university must be approved by the Study Board.
Two-educational programmes
Two-educational programmes with Mathematics as central subject in combination with a minor subject
Minor changes of the programme might occur once the concrete study plan is created. The study plan will always be in accordance with the guidelines for the academic minimum required standards for university programmes directed at teaching.
Individual plans must be approved by the two Study Boards involved.
Offered as:
2-professional | |||||
| Study programme: Mathematics as a central subject in combination with af minor subject | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation method | Assessment method |
1 Semester
| |||||
| Statistical Modelling and Analysis | Project | 15 | 7-point grading scale | External examination | Oral exam based on a project |
| Statistical Inference for Linear Models | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Computeralgebra | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Differential Geometry | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
2 Semester
| |||||
| Mathematics with Applications | Project | 15 | 7-point grading scale | External examination | Oral exam based on a project |
| Integration Theory | Course | 5 | 7-point grading scale | External examination | Written or oral exam |
| MAT8 elective courses | Course | 10 | |||
4 Semester
| |||||
| Master’s Thesis. 30 ECTS | Project | 30 | 7-point grading scale | External examination | Oral exam based on a project |
The student selects courses equivalent to 10 ECTS on the 2'nd semester (MAT8/MAT8M). Only a limited number of elective courses will be offerede each semester.
MAT8 elective courses | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation Method | Assessment method |
| Bayesian Inference and Mixed Models | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Time Series and Econometrics | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Spatial Statistics and Markov Chain Monte Carlo Methods | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Graph Theory | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Coding Theory | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Applied Harmonic Analysis | Course | 5 | Passed/Not Passed | Internal examination | Oral exam |
| Operators on Hilbert Spaces | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Algebraic Topology | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Quantitative Finance and Computational Statistics | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Financial Engineering | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Data Mining | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Compressive Sensing | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
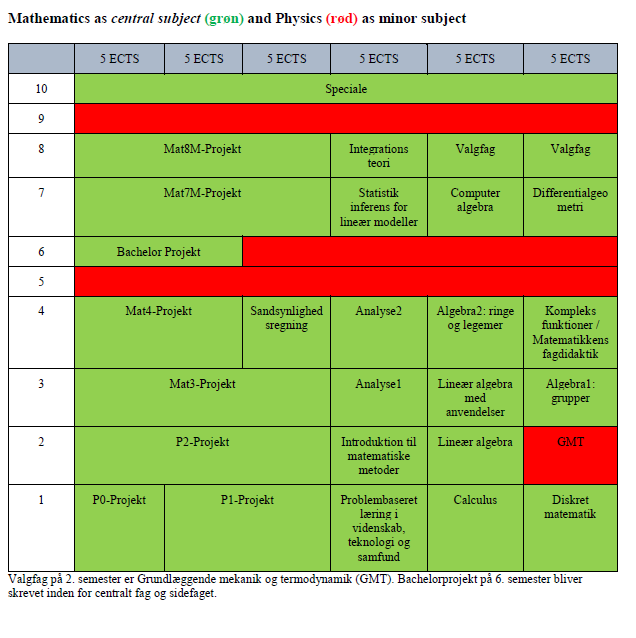
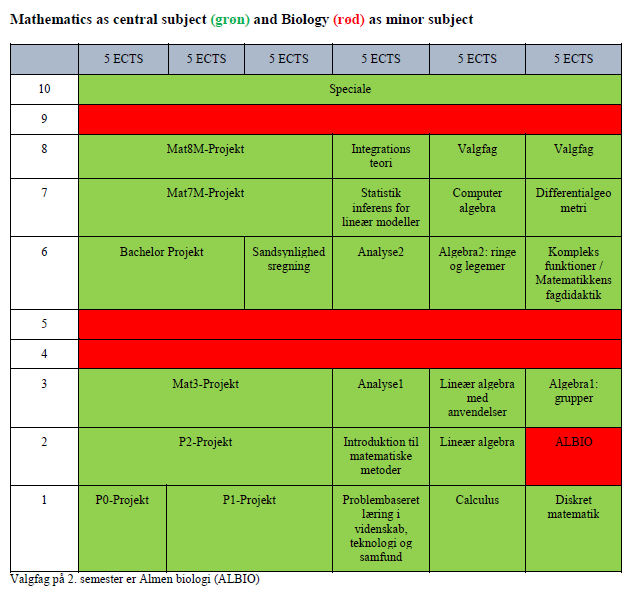
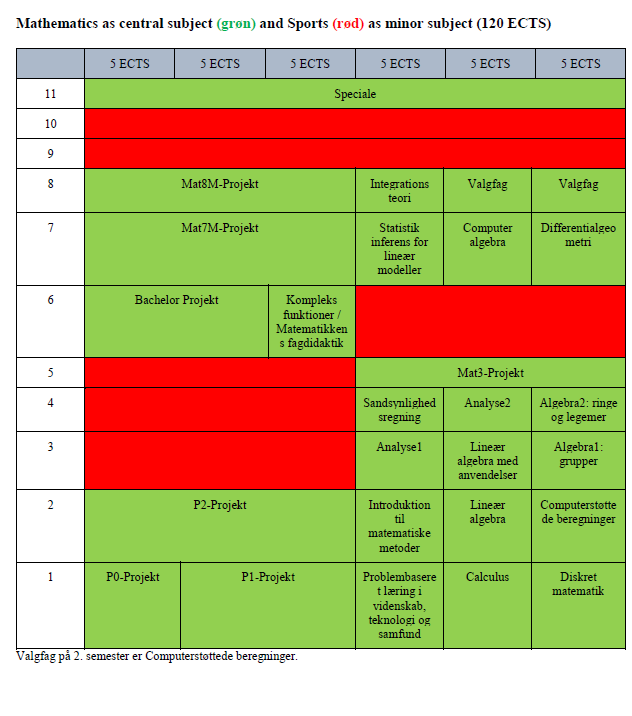
Overview over the different combinations:
The most used combinations of central and minor subjects are described in the curricula. There are, however, other combinations available.
Should you be interested in another combination than the ones depicted here, the study board will compile a concrete study programme upon inquiry.
On this website, you can read more about the various to-educational programs offered by Aalborg University https://www.aau.dk/uddannelser/bliv-gymnasielaerer/
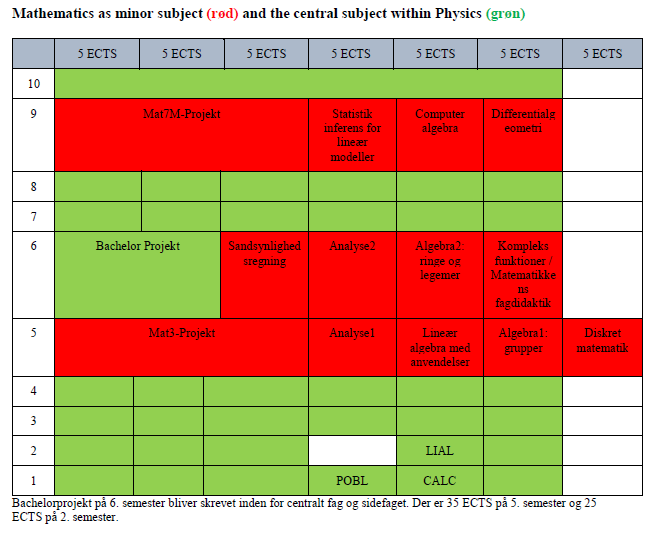
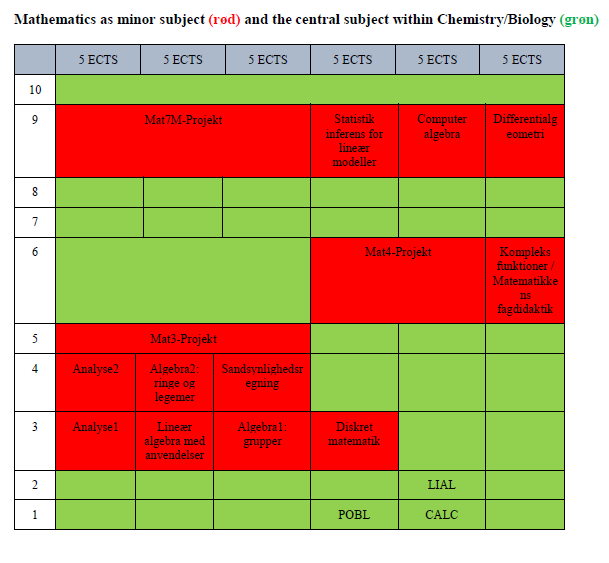
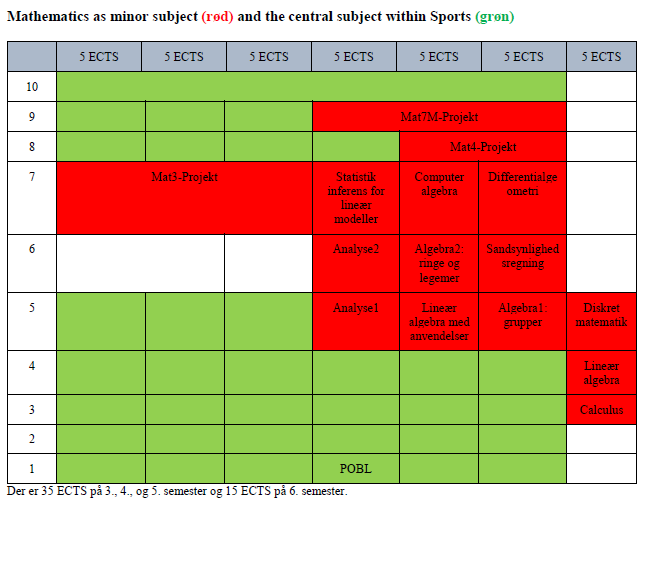
Two-educational programmes with mathematics as minor subject in combination with central subject
Tofagsuddannelse med matematik som sidefag, centralt fag inden for det naturvidenskabelige hovedområde (NAT og Idræt)
Minor changes of the programme might occur once the concrete study plan is created. The study plan will always be in accordance with the guidelines for the academic minimum required standards for university programmes directed at teaching.
Individual plans must be approved by the two Study Boards involved.
Offered as:
2-professional | |||||
| Study programme: Minor subject Mathematics in combination with central subject | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation method | Assessment method |
3 Semester
| |||||
| Statistical Modelling and Analysis | Project | 15 | 7-point grading scale | External examination | Oral exam based on a project |
| Statistical Inference for Linear Models | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Computeralgebra | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Differential Geometry | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
4 Semester
| |||||
Overview over the different combinations:
Tofagsuddannelse med matematik som sidefag, centralt fag inden for det humanistiske/samfundsvidenskabelige hovedområde (HUM/SAMF, studietidsforlængelse)
Individual plans must be approved by the two Study Boards involved.
Offered as:
2-professional | |||||
| Study programme: Minor subject Mathematics, major subject HUM/SAMF (studietidsforlængelse) | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation method | Assessment method |
1 Semester
| |||||
| Ordinary Differential Equations | Project | 15 | 7-point grading scale | Internal examination | Oral exam based on a project |
| Analysis 1 | Course | 5 | 7-point grading scale | External examination | Written or oral exam |
| Linear Algebra with Applications | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Algebra 1: Groups | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
2 Semester
| |||||
| Symmetry | Project | 10 | 7-point grading scale | External examination | Oral exam based on a project |
| Probability Theory | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Analysis 2 | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
| Algebra 2: Rings and Fields | Course | 5 | 7-point grading scale | External examination | Written or oral exam |
| MAT4. Elective courses | Course | 5 | |||
3 Semester
| |||||
| Statistical Inference for Linear Models | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Computeralgebra | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| Differential Geometry | Course | 5 | 7-point grading scale | Internal examination | Written or oral exam |
MAT4. Elective courses | |||||
| Module name | Course type | ECTS | Applied grading scale | Evaluation Method | Assessment method |
| Complex Functions | Course | 5 | Passed/Not Passed | Internal examination | Written or oral exam |
| The Didactics of Mathematics | Course | 5 | Passed/Not Passed | Internal examination | Oral exam |
19: Additional information
All students who have not participated in Aalborg University’s PBL introductory course during their Bachelor’s degree must attend the introductory course “Problem-based Learning and Project Management”. The introductory course must be approved before the student can participate in the project exam. For further information, please see the School of Engineering and Science’ website.
20: Commencement and transitional rules
The curriculum is approved by the dean and enters into force as of September 2018.
Students who wish to complete their studies under the previous curriculum from 2017 must conclude their education by the summer examination period 2019 at the latest, since examinations under the previous curriculum are not offered after this time.